Advertisements
Advertisements
Question
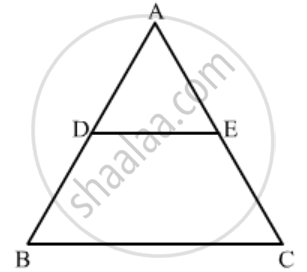
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
Options
3 : 4
9 : 16
3 : 5
9 : 25
Solution
Given: In ΔABC, D is on side AB and point E is on side AC, such that BCED is a trapezium. DE: BC = 3:5.
To find: Calculate the ratio of the areas of ΔADE and the trapezium BCED.
In ΔADE and ΔABC,
\[\angle ADE = \angle B \left( \text{Corresponding angles} \right)\]
\[\angle A = \angle A \left( \text{Common} \right)\]
\[ \therefore ∆ ADE~ ∆ ABC \left( \text{AA Similarity} \right)\]
We know that
`(Ar(Δ ADE))/(Ar(ΔABC))=(DE)^2/(BC)^2`
`(Ar(Δ ADE))/(Ar(ΔABC))= 3^2/5^2`
`(Ar(Δ ADE))/(Ar(ΔABC))= 9/25`
Let Area of ΔADE = 9x sq. units and Area of ΔABC = 25x sq. units
`Ar [trap BCED]=Ar(Δ ABC) - Ar (Δ ADE)`
`= 25x -9x`
`16x`sq units
`Now ,`
`(Ar(Δ ADE))/(Ar(trapBCED))= (9x)/(16x)`
`(Ar(Δ ADE))/(Ar(trapBCED))= 9/16`
Hence the correct answer is `b`.
APPEARS IN
RELATED QUESTIONS
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
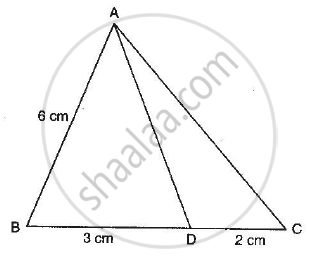
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
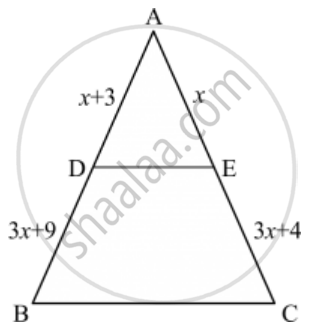
In the given figure, the value of x for which DE || AB is
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
