Advertisements
Advertisements
Question
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
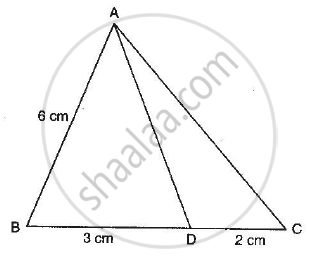
Solution
GIVEN: AB = 6cm, BD = 3cm and DC = 2cm. Also, AD is the bisector of ∠ A..
TO FIND: AC
SOLUTION: We know that the internal bisector of a triangle divides the opposite side internally in the ratio of the sides containing the angle. Therefore,
`(AB)/(AC)=(BD)/(DC)`
`6/(AC)=3/2`
`AC=(6xx2)/3`
`AC = 4cm`
APPEARS IN
RELATED QUESTIONS
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
