Advertisements
Advertisements
Question
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
Solution
In trapezium ABCD, AB || DC. P and Q are points on sides AD and BC such that PQ || AB.
Join AC. Suppose AC intersects PQ in O.
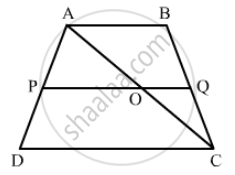
In Δ ACD , OP || CD
`∴ (AP)/(PD)=(AO)/(OC)`.......(1) (BPT)
`In Δ Abc , OQ||AB`
`∴ (BQ)/(QC)=(AO)/(OC)`.......(2) (BPT)
From (1) and (2), we get
`(AP)/(DP)=(BQ)/(QC)`
`(AP)/(18)=(35)/(15)`
`AP=(35xx18)/(5xx3)`
`AP=(7xx5xx3xx6)/(5xx3)`
`AP=(7xxcancel5xxcancel3xx6)/(cancel5xxcancel3)`
`AP = 42`
`AD=AP+PD`
`AD=42+18`
`AD=60`
Hence, the value of AD is 60 .
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
