Advertisements
Advertisements
Question
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
Options
2 : 1
1 : 2
4 : 1
1 : 4
Solution
Given: ΔABC and ΔBDE are two equilateral triangles such that D is the midpoint of BC.
To find: Ratio of areas of ΔABC and ΔBDE.
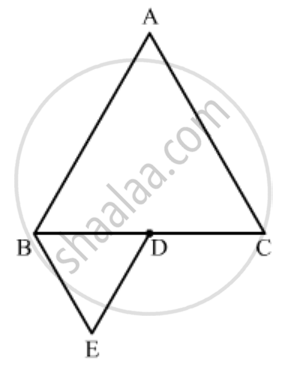
ΔABC and ΔBDE are equilateral triangles; hence they are similar triangles.
Since D is the midpoint of BC, BD = DC.
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=((BC)/(BD))^2`
`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=((BD+DC)/(BD))^2`[D is the midpoint of BC]
`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=((BD+DC)/(BD))^2`
`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=((2BD)/(BD))^2`
`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=4/1`
Hence the correct answer is `C`
APPEARS IN
RELATED QUESTIONS
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
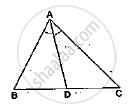
In the given figure, DE || BD. Determine AC and AE.

In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
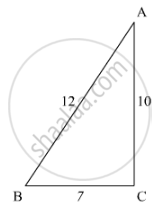
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
