Advertisements
Advertisements
Question
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
Options
50°
60°
70°
80°
Solution
Given: If ΔABC and ΔDEF are similar triangles such that
`∠A=47^o`
`∠ E=83^o`
To find: Measure of angle C
In similar ΔABC and ΔDEF,
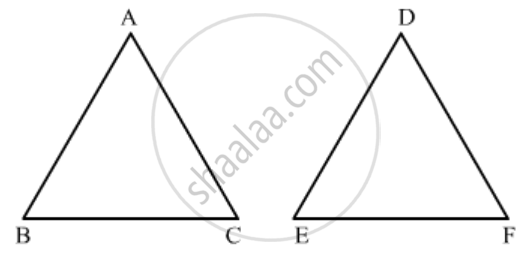
`∠ A=∠D=47^o`
`∠B=∠E=83^o`
`∠C=∠F`
We know that sum of all the angles of a triangle is equal to 180°.
`
We know that sum of all the angles of a triangle is equal to 180°.
`∠ A+∠B+∠C=180^o`
`∠B+83^o +∠C=180^o`
`∠C+130^o=180^o`
`∠C=180^o-130^o`
`∠C=50^o`
Hence the correct answer is `a`
APPEARS IN
RELATED QUESTIONS
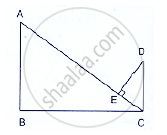
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

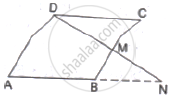
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
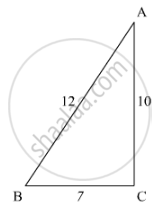
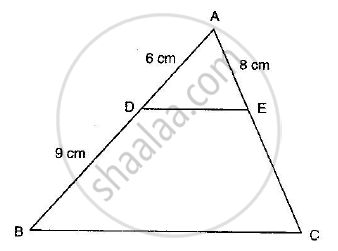
In the adjoining figure, find AC.
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
