Advertisements
Advertisements
Question
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
Options
1 : 4
1 : 2
2 : 3
4 : 5
Solution
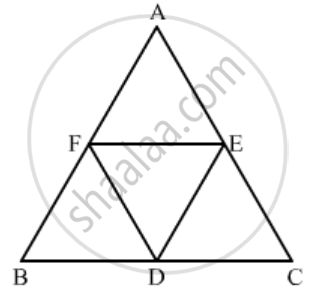
GIVEN: In ΔABC, D, E and F are the midpoints of BC, CA, and AB respectively.
TO FIND: Ratio of the areas of ΔDEF and ΔABC
Since it is given that D and, E are the midpoints of BC, and AC respectively.
Therefore DE || AB, DE || FA……(1)
Again it is given that D and, F are the midpoints of BC, and, AB respectively.
Therefore, DF || CA, DF || AE……(2)
From (1) and (2) we get AFDE is a parallelogram.
Similarly we can prove that BDEF is a parallelogram.
Now, in ΔADE and ΔABC
`∠FDE=∠A\text{(opposite angles of}||^(gm)AFDE)`
`∠DEF = ∠ B=\text{(opposite angles of}||^(gm)BDEF)`
`⇒ Δ ABC ∼ Δ DEF (\text{AA similarity criterion})`
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`{ar(Δ DEF)}/{ar(Δ ABC)}=((DE)/(AB))^2`
`{ar(Δ DEF)}/{ar(Δ ABC)}=((1/2(AB))/(AB))^2(Since DE =1/2AB)`
`{ar(Δ DEF)}/{ar(Δ ABC)}=(1/4)`
Hence the correct option is `a`
APPEARS IN
RELATED QUESTIONS
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
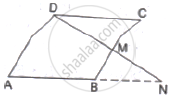
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

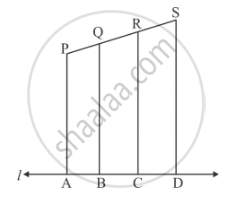
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
In the given figure, Δ AHK ∼ Δ ABC. If AK = 8 cm, BC = 3.2 cm and HK = 6.4 cm, then find the length of AC.

