Question

In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then

Options

•  ∆ABC is isosceles

• ∆ABC is equilateral

• AC = 2AB

• ∆ABC is right-angled at A

Answer 1

Given: In ΔABC,`AD ⊥ BC`, BD = 8cm, DC = 2 cm and AD = 4cm.

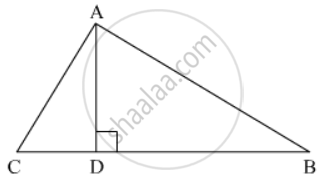
In ΔADC,

`AC^2=AD^2+DC^2`

`AC^2=4^2+2^2`

`AC^2=20`..............(1)

Similarly, in ΔADB

`AB^2=AD^2+BD^2`

`AB^2=4^2+8^2`

`AB^2=80`......................(2)

Now, In ΔABC

\[{BC}^2 = \left( CD + DB \right)^2 = \left( 2 + 8 \right)^2 = \left( 10 \right)^2 = 100\]

and

\[{AB}^2 + {CA}^2 = 80 + 20 = 100\]

\[\therefore {AB}^2 + {CA}^2 = {BC}^2\]

Hence, triangle ABC is right angled at A.

We got the result as (d)