Advertisements
Advertisements
Question
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
Solution
GIVEN: the lengths of the diagonals of a rhombus are 30 cm and 40 cm.
TO FIND: side of the rhombus.
Let the diagonals AC and CD of the rhombus ABCD meet at point O.
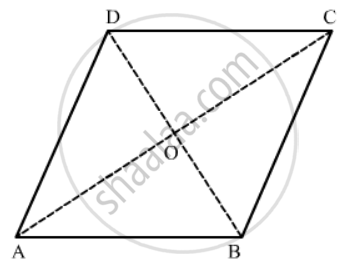
We know that the diagonals of the rhombus bisect each other perpendicularly.
Hence in right triangle AOD, by Pythagoras theorem
`\text{hypotenuse}^2+\text{perpendicular}^2+\text{base}^2`
`=15^2+20^2`
`=225+400`
`=625`
`\text{hypotenuse}=25 cm`
Hence the side of the rhombus is = 25 cm
APPEARS IN
RELATED QUESTIONS
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.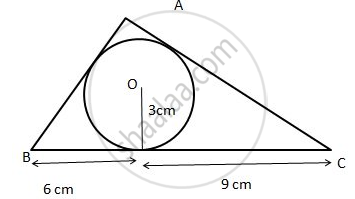
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
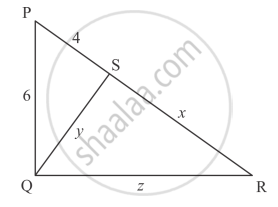
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD2 =
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
