Advertisements
Advertisements
Question
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

Solution
GIVEN: In the given figure PQ || BC, and AP: PB = 1:2
TO FIND:\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]
We know that according to basic proportionality theorem if a line is drawn parallel to one side of a triangle intersecting the other side, then it divides the two sides in the same ratio.
Since triangle APQ and ABC are similar
Hence `(AP)/(AB)=(AQ)/(AC)=(PQ)/(BC)`
Now, it is given that `(AP)/(PB)=1/2`.
`⇒ PB =2AP`
`(AP)/(AB)=(AP)/(AP+PB)=(AP)/(AP+2AP)=1/3`
Since the ratio of the areas of two similar triangle is equal to the ratio of the squares of their corresponding sides.
Hence we got the result Area (Δ APB):Area(ΔABC)=1:9
APPEARS IN
RELATED QUESTIONS
In the given figure, DE || BD. Determine AC and AE.

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
In an equilateral triangle ABC if AD ⊥ BC, then
In the given figure, if ∠ADE = ∠ABC, then CE =
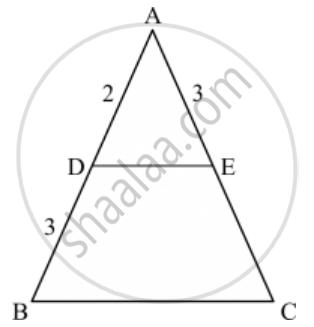
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
