Advertisements
Advertisements
Question
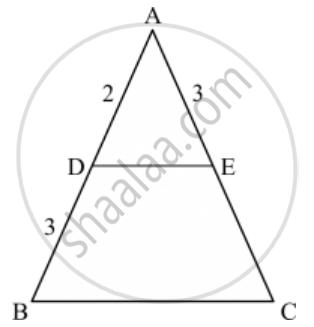
In the given figure, if ∠ADE = ∠ABC, then CE =
Options
2
5
9/2
3
Solution
Given: `∠ ADE = ∠ ABC`
To find: The value of CE
Since `∠ ADE = ∠ ABC`
∴ DE || BC (Two lines are parallel if the corresponding angles formed are equal)
According to basic proportionality theorem if a line is parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ABC, DE || BC
`(AD)/(DB)=(AE)/(EC)`
`2/3=3/EC`
`EC=(3xx3)/2`
`EC =9/2`
Hence we got the result `C`
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
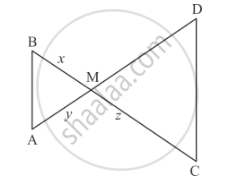
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
