Advertisements
Advertisements
प्रश्न
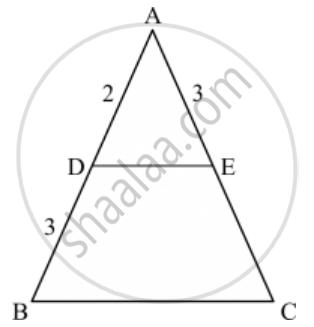
In the given figure, if ∠ADE = ∠ABC, then CE =
विकल्प
2
5
9/2
3
उत्तर
Given: `∠ ADE = ∠ ABC`
To find: The value of CE
Since `∠ ADE = ∠ ABC`
∴ DE || BC (Two lines are parallel if the corresponding angles formed are equal)
According to basic proportionality theorem if a line is parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ABC, DE || BC
`(AD)/(DB)=(AE)/(EC)`
`2/3=3/EC`
`EC=(3xx3)/2`
`EC =9/2`
Hence we got the result `C`
APPEARS IN
संबंधित प्रश्न
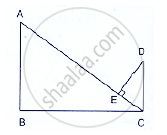
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

What values of x will make DE || AB in the given figure?

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
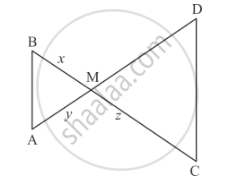
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
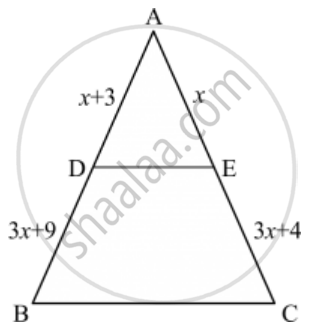
In the given figure, the value of x for which DE || AB is
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
In the given figure, Δ AHK ∼ Δ ABC. If AK = 8 cm, BC = 3.2 cm and HK = 6.4 cm, then find the length of AC.

