Advertisements
Advertisements
प्रश्न
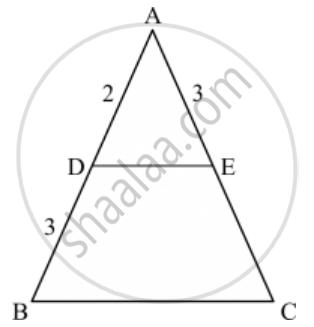
In the given figure, if ∠ADE = ∠ABC, then CE =
पर्याय
2
5
9/2
3
उत्तर
Given: `∠ ADE = ∠ ABC`
To find: The value of CE
Since `∠ ADE = ∠ ABC`
∴ DE || BC (Two lines are parallel if the corresponding angles formed are equal)
According to basic proportionality theorem if a line is parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ABC, DE || BC
`(AD)/(DB)=(AE)/(EC)`
`2/3=3/EC`
`EC=(3xx3)/2`
`EC =9/2`
Hence we got the result `C`
APPEARS IN
संबंधित प्रश्न
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
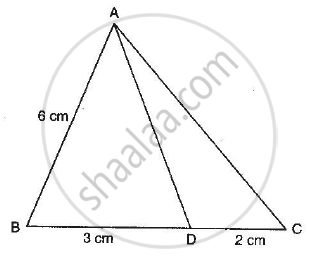
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
