Advertisements
Advertisements
प्रश्न
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
पर्याय
AB2 − AD2 = BD.DC
AB2 − AD2 = BD2 − DC2
AB2 + AD2 = BD.DC
AB2 + AD2 = BD2 − DC2
उत्तर
Given: ΔABC is an isosceles triangle, D is a point on BC such that `AD ⊥ BC`
We know that in an isosceles triangle the perpendicular from the vertex bisects the base.
∴ BD = DC
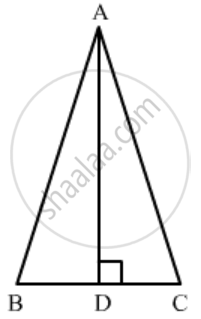
Applying Pythagoras theorem in ΔABD
`AB^2=AD^2+BD^2`
`⇒ AB^2-AD^2=BD^2`
`⇒ AB^2-AD^2=BDxxBD`
Since `BD =DC`
`⇒ AB^2-AD^2=BD xxDC`
Hence correct answer is `a`
APPEARS IN
संबंधित प्रश्न
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
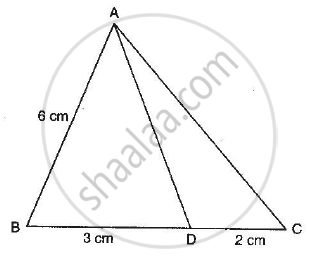
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD2 =
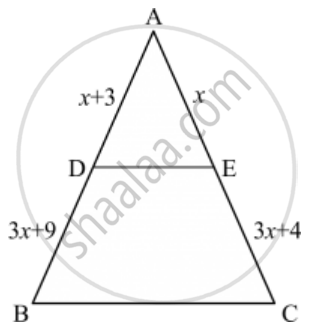
In the given figure, the value of x for which DE || AB is