Advertisements
Advertisements
प्रश्न
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD2 =
पर्याय
- \[\frac{3}{2} {DC}^2\]
2 DC2
3 CD2
4 DC2
उत्तर
Given: In an equilateral ΔABC, `AD ⊥ BC`.
Since `AD ⊥ BC`., BD = CD = \[\frac{BC}{2}\]
Applying Pythagoras theorem,
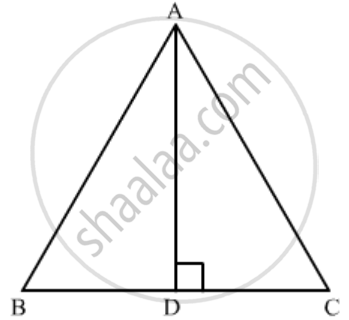
In ΔADC
`AC^2+AD^2+DC^2`
`BC^2=AD^2+DC^2`(Since AC=BC)
`(2DC)^2=AD^2+DC^2`(Since BC=2DC)
`4DC^2=AD^2+DC^2`
`3DC^2=AD^2`
`3DC^2=AD^2`
We got the result as `c`
APPEARS IN
संबंधित प्रश्न
In below figure, If AB || CD, find the value of x.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
