Advertisements
Advertisements
प्रश्न
In below figure, If AB || CD, find the value of x.
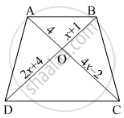
उत्तर
Since diagonals of a trapezium divide each other proportionally.
`therefore"AO"/"OC"="BO"/"OD"`
`rArr4/(4x-2)=(x+1)/(2x+4)`
⇒ 4(2𝑥 + 4) = (𝑥 + 1)(4𝑥 − 2)
⇒ 8x + 16 = x(4x – 2) +1(4x – 2)
⇒ 8x + 16 = 4x2 + 2x – 2
⇒ 4x2 + 2𝑥 − 8𝑥 − 2 − 16 = 0
⇒ 4x2 − 6𝑥 − 18 = 0
⇒ 2[2𝑥2 − 3𝑥 − 9] = 0
⇒ 2𝑥2 − 3𝑥 − 9 = 0
⇒ 2𝑥(𝑥 − 3) + 3(𝑥 − 3) = 0
⇒ (𝑥 − 3)(2𝑥 + 3) = 0
⇒ 𝑥 − 3 = 0 or 2𝑥 + 3 = 0
⇒ 𝑥 = 3 or 𝑥 = -3/2
𝑥 = -3/2 is not possible, because
`"OB"=x+1=-3/2+1=-1/2`
Length cannot be negative
`therefore"AO"/"OC"="BO"/"OD"`
APPEARS IN
संबंधित प्रश्न
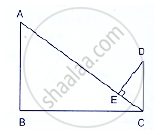
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
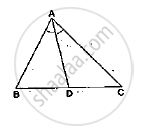
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
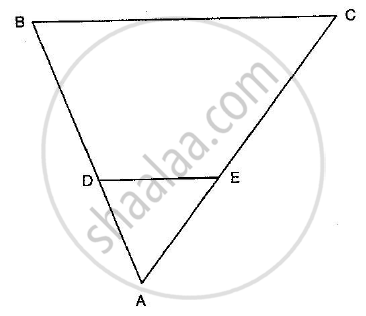
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
