Advertisements
Advertisements
प्रश्न
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
पर्याय
36 cm
30 cm
34 cm
35 cm
उत्तर
Given: ΔABC is similar to ΔDEF such that AB= 9.1cm, DE = 6.5cm. Perimeter of ΔDEF is 25cm.
To find: Perimeter of ΔABC.
We know that the ratio of corresponding sides of similar triangles is equal to the ratio of their perimeters.
Hence,
`(AB)/(DE)=(BC)/(EF)=(AC)/(DE)=(P1)/(P2)`
`(AB)/(DE)=(P(Δ ABC))/(P(Δ DEF))`
`9.1/6.5=(P(Δ ABC))/25`
`P(Δ ABC)=(9.1xx25)/6.5`
`P(Δ ABC)=35cm`
Hence the correct answer is `d`
APPEARS IN
संबंधित प्रश्न
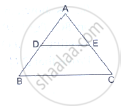
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
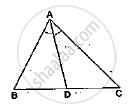
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
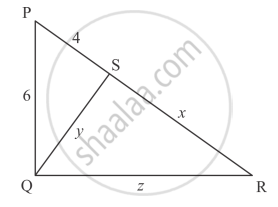
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
