Advertisements
Advertisements
प्रश्न
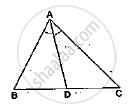
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
उत्तर
It is given that AD bisector ∠𝐴.
Applying angle – bisector theorem in Δ ABC, we get:
`(BD)/(DC)=(AB)/(AC)`
BD = 3.2 cm, BC = 6 cm
Therefore, DC = 6- 3.2 = 2.8 cm
⟹ `3.2/2.8=5.6/(AC)`
⟹ `AC=(5.6xx2.8)/3.2=4.9 cm`
APPEARS IN
संबंधित प्रश्न
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
State Pythagoras theorem and its converse.
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
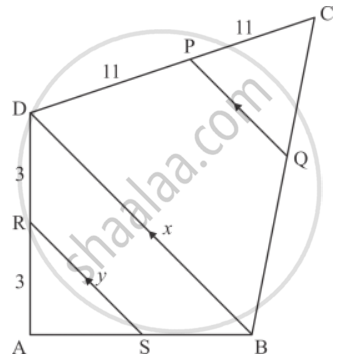
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
