Advertisements
Advertisements
प्रश्न
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
उत्तर
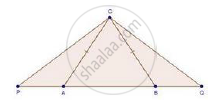
Given: In ΔABC, CA = CB and AP × BQ = AC2
To prove: ΔAPC ~ ΔBCQ
Proof:
AP × BQ = AC2 [Given]
⇒ AP × BQ = AC × AC
⇒ AP × BQ = AC × BC [AC = BC given]
`rArr"AP"/"BC"="AC"/"BQ"` ......(i)
Since, CA = CB [Given]
Then, ∠CAB = ∠CBA …(ii) [Opposite angles to equal sides]
Now, ∠CAB + ∠CAP = 180° …(iii) [Linear pair of angles]
And, ∠CBA + ∠CBQ = 180° …(iv) [Linear pair of angles]
Compare equation (ii) (iii) & (iv)
∠CAP = ∠CBQ …(v)
In ΔAPC and ΔBCQ
∠CAP = ∠CBQ [From (v)]
`"AP"/"BC"="AC"/"BQ"` [From (i)]
Then, ΔAPC~ΔBCQ [By SAS similarity]
APPEARS IN
संबंधित प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
