Advertisements
Advertisements
प्रश्न
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
उत्तर
GIVEN: Altitudes of two similar triangles are in ratio 2:3.
TO FIND: Ratio of the areas of two similar triangles.
Let first triangle be ΔABC and the second triangle be ΔPQR
We know that the areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.
`⇒ (Area(ABC))/(Area(PQR))=2^2/3^2`
` (Area(ABC))/(Area(PQR))=4/9`
APPEARS IN
संबंधित प्रश्न
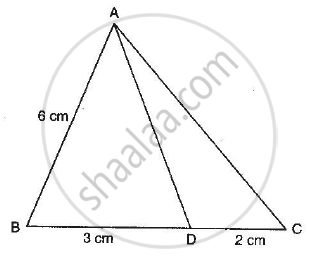
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
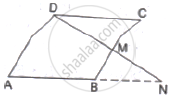
State basic proportionality theorem and its converse.
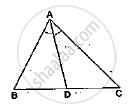
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
