Advertisements
Advertisements
प्रश्न
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
पर्याय
2:5
4 : 25
4 : 15
8 : 125
उत्तर
Given: ΔABC and ΔDEF are two triangles such that `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)=2/5`
To find: `\text{Ar(Δ ABC): Ar(Δ DEF)}`
We know that if the sides of two triangles are proportional, then the two triangles are similar.
Since `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)=2/5`, therefore, ΔABC and ΔDEF are similar.
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`\text{Ar(Δ ABC)}/\text{Ar(Δ DEF)}=(AB)^2/(DE)^2`
`\text{Ar(Δ ABC)}/\text{Ar(Δ DEF)}=2^2/5^2`
`\text{Ar(Δ ABC)}/\text{Ar(Δ DEF)}=4/25`
Hence the correct answer is `b`
APPEARS IN
संबंधित प्रश्न
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
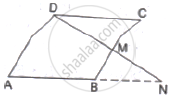
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

State AAA similarity criterion.
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
