Advertisements
Advertisements
Question
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
Options
2:5
4 : 25
4 : 15
8 : 125
Solution
Given: ΔABC and ΔDEF are two triangles such that `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)=2/5`
To find: `\text{Ar(Δ ABC): Ar(Δ DEF)}`
We know that if the sides of two triangles are proportional, then the two triangles are similar.
Since `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)=2/5`, therefore, ΔABC and ΔDEF are similar.
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`\text{Ar(Δ ABC)}/\text{Ar(Δ DEF)}=(AB)^2/(DE)^2`
`\text{Ar(Δ ABC)}/\text{Ar(Δ DEF)}=2^2/5^2`
`\text{Ar(Δ ABC)}/\text{Ar(Δ DEF)}=4/25`
Hence the correct answer is `b`
APPEARS IN
RELATED QUESTIONS
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
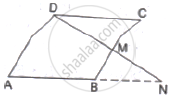
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
In the given figure, Δ AHK ∼ Δ ABC. If AK = 8 cm, BC = 3.2 cm and HK = 6.4 cm, then find the length of AC.

