Advertisements
Advertisements
Question
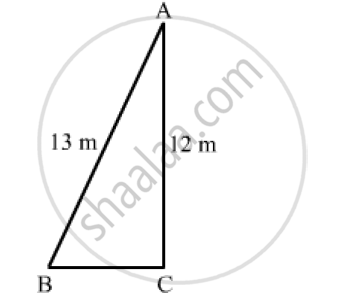
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
Solution
Let AB and AC be the ladder and height of the building.
It is given that :
AB = 13 m and AC = 12 m
We need to find distance of the foot of the ladder from the building, i.e, BC.
In right-angled triangle ABC, we have:
`AB^2=AC^2+BC^2`
⟹ `BC=sqrt(13^2-12^2)`
=`sqrt(169-144)`
`=sqrt25`
=5 m
Hence, the distance of the foot ladder from the building is 5 m
APPEARS IN
RELATED QUESTIONS
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
State AAA similarity criterion.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
