Question

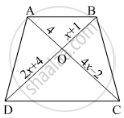
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`

Answer 1

We are given the following quadrilateral with O as the intersection point of diagonals

To Prove : `[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`

Given ACB and ACD are two triangles on the same base AC

Consider h as the distance between two parallel sides

Now we see that the height of these two triangles ACB and ACD are same and are equal to h

So

`[A(∆"ACB")]/[A(∆"ACD")] = (1/2 xx "AB" xx "h" )/(1/2 xx "CD" xx "h")`

`=("AB")/("CD")`..........(2)

Now consider the triangles AOB and COD in which

`∠ "AOB" = ∠ "COD"`

`∠ "ABO" = ∠ "ODC"` (alternative angle)

`∠ "BAO" = ∠ "DCA"` (alternative angle)

Therefore , `Δ "ODC" ∼ Δ "OBA"`

`⇒("AO")/("OC") = ("BO")/("DO")=("AB")/("CD")`

`⇒ ("BO")/("DO") = ("AB")/("CD")`

From equation (1) and (2) we get

`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`

Hence prove that `[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`