Advertisements
Advertisements
प्रश्न
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
उत्तर
We are given the following quadrilateral with O as the intersection point of diagonals

To Prove : `[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
Given ACB and ACD are two triangles on the same base AC
Consider h as the distance between two parallel sides
Now we see that the height of these two triangles ACB and ACD are same and are equal to h
So
`[A(∆"ACB")]/[A(∆"ACD")] = (1/2 xx "AB" xx "h" )/(1/2 xx "CD" xx "h")`
`=("AB")/("CD")`..........(2)
Now consider the triangles AOB and COD in which
`∠ "AOB" = ∠ "COD"`
`∠ "ABO" = ∠ "ODC"` (alternative angle)
`∠ "BAO" = ∠ "DCA"` (alternative angle)
Therefore , `Δ "ODC" ∼ Δ "OBA"`
`⇒("AO")/("OC") = ("BO")/("DO")=("AB")/("CD")`
`⇒ ("BO")/("DO") = ("AB")/("CD")`
From equation (1) and (2) we get
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
Hence prove that `[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
APPEARS IN
संबंधित प्रश्न
In the below figure, If AB || CD, find the value of x.
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In the given figure, DE || BD. Determine AC and AE.

ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
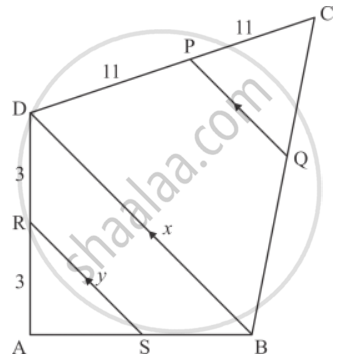
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
