Advertisements
Advertisements
प्रश्न
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
उत्तर
Given: In Δ ABC ray AD bisects angle A and intersects BC in D, If `BC = a, AC=b` and `AB =c`
To Prove:
The corresponding figure is as follows
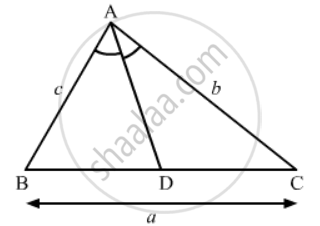
Proof: In triangle ABC, AD is the bisector of `∠ A`
Therefore `(AB)/(AC)=(BD)/(CD)`
Substitute `BC = a, AC= b` and `AB =c` we get,
`c/b=(BD)/(BC-BD)`
`c/b=(BD)/(a-BD)`
By cross multiplication we get.
`c(a-BD)=bxxBD`
`ac-cBD=bBD`
`ac=bBD+cBD`
`ac=(b+2)BD`
`(ac)/(b+c)=BD`
We proved that `BD=(ac)/(b+c)`
APPEARS IN
संबंधित प्रश्न
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
In the given figure, DE || BD. Determine AC and AE.

In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
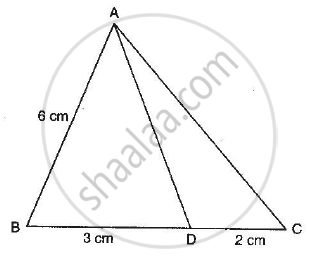
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
State AAA similarity criterion.
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
