Advertisements
Advertisements
प्रश्न
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
उत्तर
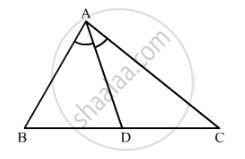
We have to find the value of BD.
Given AB = 18cm ,AC= 15cm and `BC = 22cm`.
In Δ ABC, AD the bisector of `∠ A.`.
`(AB)/(AC)=(BD)/(DC)`
`(AB)/(AC)=(BD)/(BC-BD)`
`18/15=(BD)/(22-BD)`
On cross multiplication, we get
`6(22-BD)=5xxBD`
`132-6BD=5BD`
`132=5BD+6BD`
`132=11BD`
`BD=12cm`
Hence, the value of BD is 12 cm.
APPEARS IN
संबंधित प्रश्न
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
