Advertisements
Advertisements
प्रश्न
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
पर्याय
108 cm2
96 cm2
48 cm2
100 cm2
उत्तर
Given: In Δ ABC and Δ DEF
`Δ ABC ∼ Δ DEF`
`Ar (ΔABC)=54 cm^2 `
`BC=3cm`and `EF=4cm`
To find: Ar(Δ DEF)
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`(Ar(ΔABC))/(Ar(ΔDEF))=(BC)^2/(EF)^2`
`(54)/(Ar(ΔDEF))=3^2/4^2`
`(54)/(Ar(ΔDEF))=9/6`
`(54)/(Ar(ΔDEF))= (16xx54)/9`
`Ar(ΔDEF)=96 cm^2`
Hence the correct answer is `b`
APPEARS IN
संबंधित प्रश्न
What values of x will make DE || AB in the given figure?

In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
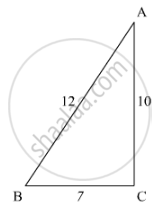
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
