Advertisements
Advertisements
प्रश्न
In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
उत्तर
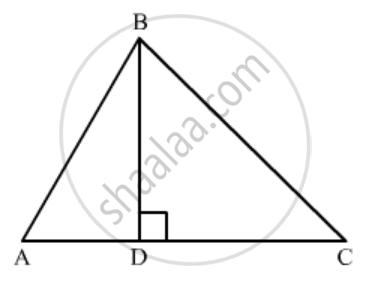
Since Δ ADB is right triangle right angled at D
`AB^2=AD^2+BD^2`
In right Δ BDC, we have
`CD^2+BD^2=BC^2`
Sine `2AC.DC=BC^2`
`⇒DC^2+BD^2=2AC.DC `
`2AC.DC=AC^2-AC^2+DC^2+BD^2`
`AC^2=AC^2+DC^2-2AC.DC+BD^2`
`AC^2=(AC-DC)^2+BD^2`
`AC^2=AD^2+BD^2`
Now substitute `AD^2+BD^2=AB^2`
`AC^2=AB^2`
`AC=AB`
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
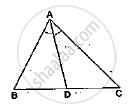
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the road. Assuming that her string (from the tip of her road to the fly) is taut, how much string does she have out (in the given figure)? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
In an equilateral triangle ABC if AD ⊥ BC, then
