Advertisements
Advertisements
Question
In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
Solution
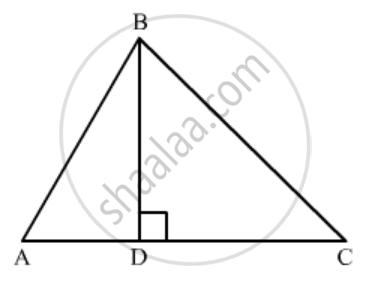
Since Δ ADB is right triangle right angled at D
`AB^2=AD^2+BD^2`
In right Δ BDC, we have
`CD^2+BD^2=BC^2`
Sine `2AC.DC=BC^2`
`⇒DC^2+BD^2=2AC.DC `
`2AC.DC=AC^2-AC^2+DC^2+BD^2`
`AC^2=AC^2+DC^2-2AC.DC+BD^2`
`AC^2=(AC-DC)^2+BD^2`
`AC^2=AD^2+BD^2`
Now substitute `AD^2+BD^2=AB^2`
`AC^2=AB^2`
`AC=AB`
APPEARS IN
RELATED QUESTIONS
In below figure, If AB || CD, find the value of x.
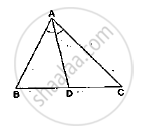
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
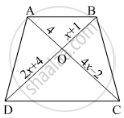
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
