Advertisements
Advertisements
Question
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

Solution
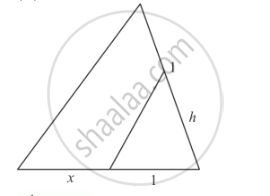
`1/(1+h)=x/(x+1)`
By cross multiplication on both sides, we get
`1xx(x+1)=x xx(1+h)`
`x+1=x+hx`
`x+1-x=hx`
`cancelx+1-cancelx=hx`
`1=xh`
`1/h=x`
Hence the value of x is `1/h`.
APPEARS IN
RELATED QUESTIONS
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
State Pythagoras theorem and its converse.
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD2 =
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
