Advertisements
Advertisements
Question
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
Solution
We have the following figure.

Let Draw an altitude AD on Extended BC
In ∆ADC, ∠D = 90°
Therefore, by Pythagoras theorem, we have
`AC^2=AD^2+DC^2`
`AC^2=AD^2+(DB+BC)^2`
`AC^2=AD^2+DB^2+BC^2+2.BC.BD` ...(i)
In ΔADB, ∠D = 90°
⇒ `AD^2 + BD^2 = AB^2`
By substituting values of equation (i)
⇒`AD^2+DB^2+BC^2+2.BC.BD = AC^2`
⇒`AB^2 + BC^2 + 2BD.BC = AC^2`
As in ΔADB, ∠DAB = 45°
⇒ AD = DB (Opposite sides are equal)
⇒`AB^2+BC^2+2.BC.BD = AC^2`
⇒`AB^2+BC^2+2.BC.AD = AC^2`
⇒`AB^2+BC^2 + 4 xx 2/4 xx AD xx BC= AC^2`
∴ `1/2 xx AD xx BC = ar(ΔABC)`
⇒ `AC^2 = AB^2 + BC^2 + 4 ar (∆ABC)`
APPEARS IN
RELATED QUESTIONS
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
What values of x will make DE || AB in the given figure?

In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
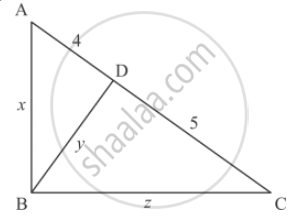
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
