Advertisements
Advertisements
Question
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
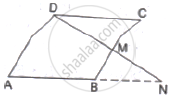
Solution
(i) Given: ABCD is a parallelogram
To prove :
(1)`(DM)/(MN)=(DC)/(BN)`
(2) `(DN)/(DM)=(AN)/(DC)`
Proof: In Δ DMC and Δ NMB
∠DMC = ∠NMB (Vertically opposite angle)
∠DCM = ∠NBM (Alternate angles)
By AAA- Similarity
ΔDMC ~ ΔNMB
∴`( DM)/(MN)=(DC)/(BM)`
NOW, `(MN)/(DM)+(BN)/(DC)`
Adding 1 to both sides, we get
`(MN)/(DM)+1=(BN)/(DC)+1`
⟹ `(MN+DM)/(DM)=(BN+DC)/(DC)`
⟹ `(MN+DM)/(DM)=(BN+AB)/(DC)` [∵ ABCD is a parallelogram]
⟹ `(DN)/(DM)=(AN)/(DC)`
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

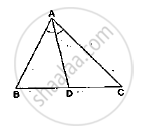
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
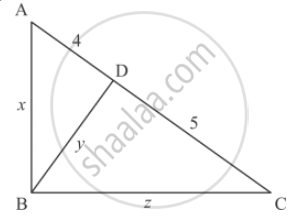
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
