Advertisements
Advertisements
Question
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

Solution
We have:
`(AD)/(DE)=5.7/9.5=0.6 cm`
`(AE)/(EC)=4.8/8=0.6 cm`
Hence,`(AD)/(DB)=(AE)/(EC)`
Applying the converse of Thales’ theorem,
We conclude that DE || BC
APPEARS IN
RELATED QUESTIONS
In the below figure, If AB || CD, find the value of x.
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
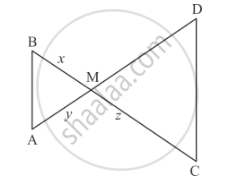
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
