Advertisements
Advertisements
Question
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

Solution
In ΔACB, by Pythagoras theorem
AB2 = AC2 + BC2
⇒ AB2 = (5)2 + (12)2
⇒ AB2 = 25 + 144 = 169
⇒ AB = `sqrt169` = 13 cm
In ΔAED and ΔACB
∠A = ∠A [Common]
∠AED = ∠ACB [Each 90°]
Then, ΔAED ~ ΔACB [By AA similarity]
`therefore"AE"/"AC"="DE"/"CB"="AD"/"AB"` [Corresponding parts of similar Δ are proportional]
`rArr"AE"/5="DE"/12=3/13`
`rArr"AE"/5=3/13` and `"DE"/12=3/13`
`"AE"=15/13` cm and `"DE"=36/13` cm
APPEARS IN
RELATED QUESTIONS
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
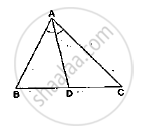
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
What values of x will make DE || AB in the given figure?

In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
