Advertisements
Advertisements
प्रश्न
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

उत्तर
In ΔACB, by Pythagoras theorem
AB2 = AC2 + BC2
⇒ AB2 = (5)2 + (12)2
⇒ AB2 = 25 + 144 = 169
⇒ AB = `sqrt169` = 13 cm
In ΔAED and ΔACB
∠A = ∠A [Common]
∠AED = ∠ACB [Each 90°]
Then, ΔAED ~ ΔACB [By AA similarity]
`therefore"AE"/"AC"="DE"/"CB"="AD"/"AB"` [Corresponding parts of similar Δ are proportional]
`rArr"AE"/5="DE"/12=3/13`
`rArr"AE"/5=3/13` and `"DE"/12=3/13`
`"AE"=15/13` cm and `"DE"=36/13` cm
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In the given figure, DE || BD. Determine AC and AE.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
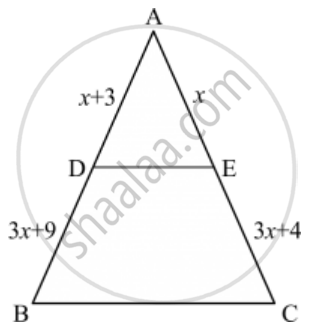
In the given figure, the value of x for which DE || AB is
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
