Advertisements
Advertisements
प्रश्न
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
विकल्प
∆FDE ∼ ∆CAB
∆FDE ∼ ∆ABC
∆CBA ∼ ∆FDE
∆BCA ∼ ∆FDE
उत्तर
We know that if two triangles are similar if their corresponding sides are proportional.

It is given that ΔABC and ΔDEF are two triangles such that
`(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`.
\[\angle A = \angle D\]
\[\angle B = \angle E\]
\[\angle C = \angle F\]
∴ ΔCAB ∼ ΔFDE
Hence the correct answer is `a`.
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
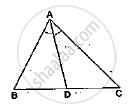
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
