Advertisements
Advertisements
प्रश्न
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
विकल्प
∠A = ∠F
∠A = ∠D
∠B = ∠D
∠B = ∠E
उत्तर
Given: In ΔABC and ΔDEF, `(AB)/(DE)=(BC)/(FD)`.
We know that if in two triangles, one pair of corresponding sides are proportional and the included angles are equal, then the two triangles are similar.
Then, `∠B=∠D`

Hence, ΔABC is similar to ΔDEF, we should have .`∠B=∠D`
Hence the correct answer is `c`
APPEARS IN
संबंधित प्रश्न
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

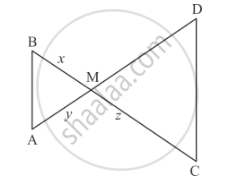
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
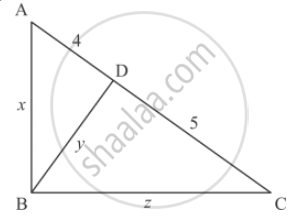
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
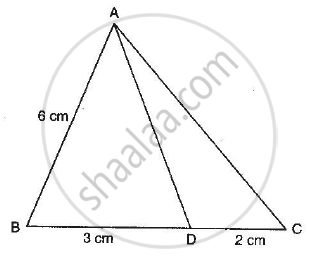
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
