Advertisements
Advertisements
प्रश्न
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
विकल्प
12 cm
8 cm
- \[8\sqrt{2} cm\]
- \[12\sqrt{2} cm\]
उत्तर
Given: One side of isosceles right triangle is 4√2cm
To find: Length of the hypotenuse.
We know that in isosceles triangle two sides are equal.

In isosceles right triangle ABC, let AB and AC be the two equal sides of measure 4√2cm.
Applying Pythagoras theorem, we get
`BC^2=AB^2+AC^2`
`BC^2=(4sqrt2)^2+(4sqrt2)^2`
`BC^2=32+32`
`BC^2=64`
`BC=8`
Hence correct answer is `b`.
APPEARS IN
संबंधित प्रश्न
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
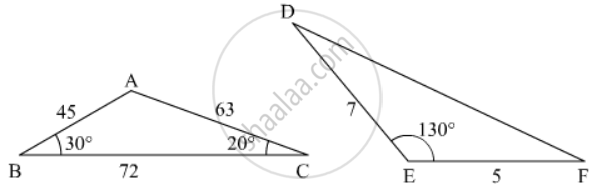
In the given figure the measure of ∠D and ∠F are respectively
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
