Advertisements
Advertisements
प्रश्न
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
विकल्प
- \[6\sqrt{2} cm\]
6 cm
- \[2\sqrt{6} cm\]
- \[4\sqrt{2} cm\]
उत्तर
Given: In an isosceles ΔABC, `∠C= 90^o`, AC = 6 cm.
To find: AB
In an isosceles ΔABC, `∠C= 90^o`,.
Therefore, BC = AC = 6 cm
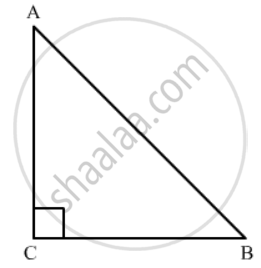
Applying Pythagoras theorem in ΔABC, we get
`AB^2=AC^2+BC^2`
`AB^2=6^2+6^2(AC=BC)`(Side of isosceles triangle)
`AB^2=36+36`
`AB^2=72`
`AB= 6sqrt2 cm`
We got the result as `a`.
APPEARS IN
संबंधित प्रश्न
In the given figure, DE || BD. Determine AC and AE.

The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
