Advertisements
Advertisements
प्रश्न
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
उत्तर
In ΔABC, in which ∠A is an acute angle with 60°.

`sin 60^o = (CD)/(AC)=sqrt3/2`
`⇒ CD = sqrt3/2AC`.................(1)
`cose 60^o = (AD)/(AC)=1/2`
`⇒ AD = 1/2 AC`
Now apply Pythagoras' theorem in triangle BCD
`BC^2=CD^2+BD^2`
`= CD^2 +(AB-AD)^2`
`= (sqrt3/2AC)^2+AB^2+(1/2AC)^2-2AB1/2AC`
`=AC^2+AB^2-AB.AC`
Hence `BC^2=AB^2+AC^2-AB.AC`
APPEARS IN
संबंधित प्रश्न
In the given figure, DE || BD. Determine AC and AE.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
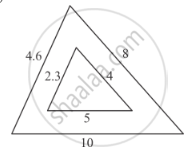
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
