Advertisements
Advertisements
प्रश्न
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
विकल्प
31 m
17 m
25 m
26 m
उत्तर
A man goes 24m due to west and then 7m due north.
Let the man starts from point B and goes 24 m due to west and reaches point A, then walked 7m north and reaches point C.
Now we have to find the distance between the starting point and the end point i.e. BC.
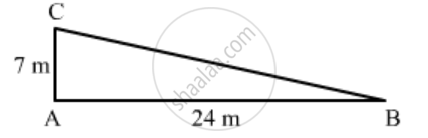
In right triangle ABC, applying Pythagoras theorem, we get
`BC^2=AB^2+AC^2`
`BC^2=(24)^2+(7)^2`
`BC^2=576+49`
`BC^2=625`
`BC=25m`
Hence correct answer is `c`.
APPEARS IN
संबंधित प्रश्न
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
