Advertisements
Advertisements
प्रश्न
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
उत्तर
GIVEN: the lengths of the diagonals of a rhombus are 30 cm and 40 cm.
TO FIND: side of the rhombus.
Let the diagonals AC and CD of the rhombus ABCD meet at point O.
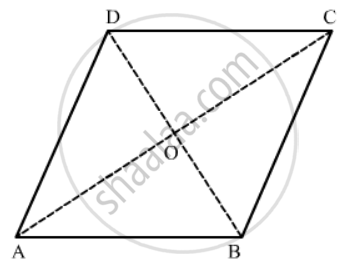
We know that the diagonals of the rhombus bisect each other perpendicularly.
Hence in right triangle AOD, by Pythagoras theorem
`\text{hypotenuse}^2+\text{perpendicular}^2+\text{base}^2`
`=15^2+20^2`
`=225+400`
`=625`
`\text{hypotenuse}=25 cm`
Hence the side of the rhombus is = 25 cm
APPEARS IN
संबंधित प्रश्न
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.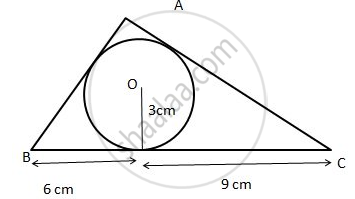
What values of x will make DE || AB in the given figure?

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
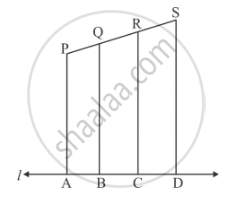
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
