Advertisements
Advertisements
प्रश्न
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that
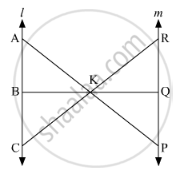
उत्तर
Three pair of similar triangles are-
(ii) Since the pair of similar triangles mentioned above can give us the desired result. The ratios of the corresponding side of the similar triangle are equal.
So,
`Δ ABK ≈ Δ PQK`
Therefore,
`(AB)/(PQ)=(AK)/(PK)=(BK)/(QK)` ……equation (1)
Similarly in ,`Δ CBK ≈ Δ RQK` ……equation (2)
Similarly ,`Δ ACK ≈ Δ PRK`
`(AC)/(PQ)=(AK)/(PK)=(CK)/(RK)`……equation (3)
From the above equations 1 and 2 we have,
`(AB)/(PQ)=(AK)/(PK)=(BK)/(QK)=(CB)/(RQ)=(CK)/(RK)`
`⇒ (AB)/(PQ)=(CB)/(RQ)……eqaution (4)`
`⇒ (AB)/(CB)=(PQ)/(RQ)`
`⇒ (AB)/(CB)+1=(PQ)/(RQ)+1`
`⇒ (AC)/(CB)=(PR)/(RQ)`
`⇒ (AC)/(CB)=(PR)/(RQ)`
`⇒ (AC)/(PR)=(CB)/(RQ)`
Combining it with equation (4)
`(AC)/(PR)=(CB)/(RQ)=(AB)/(PQ)`
hence proved
`(AC)/(PR)=(AB)/(PQ)=(BC)/(RQ)`
APPEARS IN
संबंधित प्रश्न
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In the given figure,
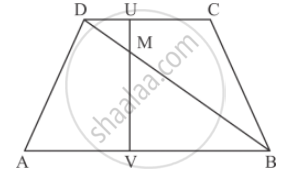
AB || DC prove that
(i) ∆DMU ∼ ∆BMV
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
State SSS similarity criterion.
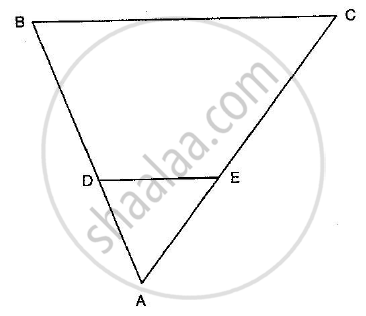
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
In the given figure the measure of ∠D and ∠F are respectively
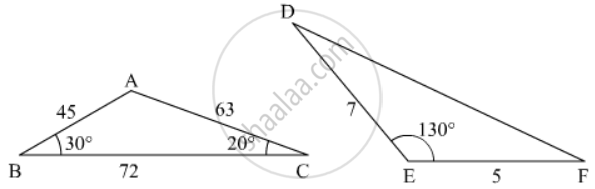
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
