Advertisements
Advertisements
प्रश्न
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

उत्तर
Three pair of similar triangles are-
(ii) Since the pair of similar triangles mentioned above can give us the desired result. The ratios of the corresponding side of the similar triangle are equal.
So,
`Δ ABK ≈ Δ PQK`
Therefore,
`(AB)/(PQ)=(AK)/(PK)=(BK)/(QK)` ……equation (1)
Similarly in ,`Δ CBK ≈ Δ RQK` ……equation (2)
Similarly ,`Δ ACK ≈ Δ PRK`
`(AC)/(PQ)=(AK)/(PK)=(CK)/(RK)`……equation (3)
From the above equations 1 and 2 we have,
`(AB)/(PQ)=(AK)/(PK)=(BK)/(QK)=(CB)/(RQ)=(CK)/(RK)`
`⇒ (AB)/(PQ)=(CB)/(RQ)……eqaution (4)`
`⇒ (AB)/(CB)=(PQ)/(RQ)`
`⇒ (AB)/(CB)+1=(PQ)/(RQ)+1`
`⇒ (AC)/(CB)=(PR)/(RQ)`
`⇒ (AC)/(CB)=(PR)/(RQ)`
`⇒ (AC)/(PR)=(CB)/(RQ)`
Combining it with equation (4)
`(AC)/(PR)=(CB)/(RQ)=(AB)/(PQ)`
hence proved
`(AC)/(PR)=(AB)/(PQ)=(BC)/(RQ)`
APPEARS IN
संबंधित प्रश्न
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.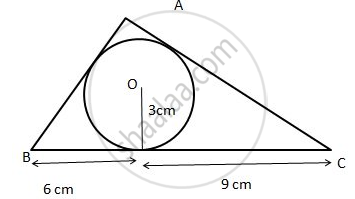
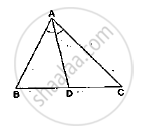
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
State SSS similarity criterion.
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
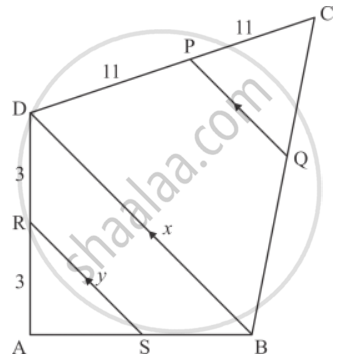
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
