Advertisements
Advertisements
प्रश्न
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
पर्याय
- \[\frac{13}{2}cm\]
- \[\frac{60}{13}cm\]
- \[\frac{13}{60}cm\]
- \[\frac{2\sqrt{15}}{13}cm\]
उत्तर
Given: In ΔABC, `∠ A = 90^o` AD ⊥ BC, AC = 12cm, and AB = 5cm.
To find: AD
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
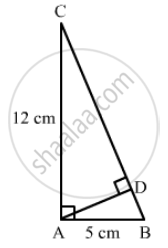
In ∆ACB and ∆ADC,
We got the result as `b`.
APPEARS IN
संबंधित प्रश्न
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
State basic proportionality theorem and its converse.
State SSS similarity criterion.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

In an equilateral triangle ABC if AD ⊥ BC, then
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
