Advertisements
Advertisements
प्रश्न
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
उत्तर
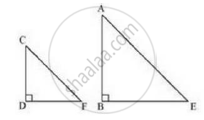
Let AB be a tower
CD be a stick, CD = 6m
Shadow of AB is BE = 28m
Shadow of CD is DF = 4m
At same time light rays from sun will fall on tower and stick at same angle.
So, ∠DCF = ∠BAE
And ∠DFC = ∠BEA
∠CDF = ∠ABE (tower and stick are vertical to ground)
Therefore Δ ABE ~ ΔCDF (By AA similarity)
So,
`"AB"/"CD"="BE"/"DF"`
`"AB"/6=28/4`
`"AB"=28xx6/4=42` m
So, height of tower will be 42 metres.
APPEARS IN
संबंधित प्रश्न
What values of x will make DE || AB in the given figure?

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
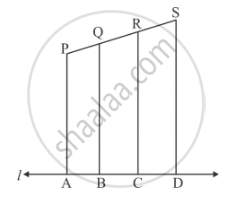
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
State Pythagoras theorem and its converse.
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
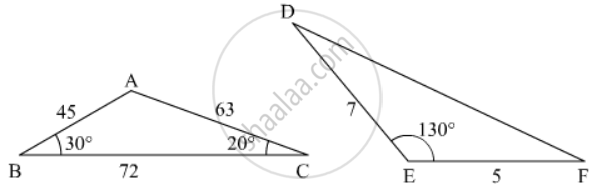
In the given figure the measure of ∠D and ∠F are respectively
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
