Advertisements
Advertisements
प्रश्न
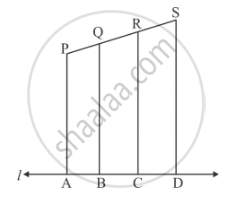
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
उत्तर
Given `AB = 6cm ,BC = 9cm,CD= 12cm,AD=27cm ` and `PS = 36cm`
PA, QB, RC and SD is perpendicular to l,
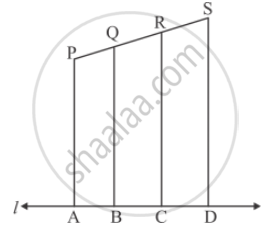
Therefore, by the corollory of basic proportionality theorem, we have
`(AB)/(AD)=(PQ)/(PS)`
`(BC)/(AD)=(QR)/(PS)`
`(CD)/(AD)=(RS)/(PS)`
`⇒ (AB)/(AD)=(PQ)/(PS)`
`6/27=(PQ)/36`
`(6xx36)/27=PQ`
`PQ = 8`
Now for QR
`(BC)/(AD)=(QR)/(PS)`
`(9)/(27)=(QR)/(36)`
`(6xx36)/27=QR`
`QR=12`
Again for RS
`(CD)/(AD)=(RS)/(PS)`
`12/27=(RS)/36`
`(12xx36)/27=RS`
`RS = 16`
Hence, the values of PQ, QR and RS are `8,12,16`respectively.
APPEARS IN
संबंधित प्रश्न
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In the adjoining figure, find AC.
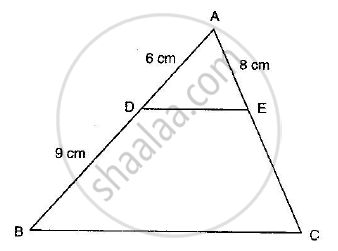
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
