Advertisements
Advertisements
Question
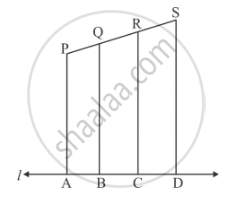
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
Solution
Given `AB = 6cm ,BC = 9cm,CD= 12cm,AD=27cm ` and `PS = 36cm`
PA, QB, RC and SD is perpendicular to l,
Therefore, by the corollory of basic proportionality theorem, we have
`(AB)/(AD)=(PQ)/(PS)`
`(BC)/(AD)=(QR)/(PS)`
`(CD)/(AD)=(RS)/(PS)`
`⇒ (AB)/(AD)=(PQ)/(PS)`
`6/27=(PQ)/36`
`(6xx36)/27=PQ`
`PQ = 8`
Now for QR
`(BC)/(AD)=(QR)/(PS)`
`(9)/(27)=(QR)/(36)`
`(6xx36)/27=QR`
`QR=12`
Again for RS
`(CD)/(AD)=(RS)/(PS)`
`12/27=(RS)/36`
`(12xx36)/27=RS`
`RS = 16`
Hence, the values of PQ, QR and RS are `8,12,16`respectively.
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

What values of x will make DE || AB in the given figure?

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
State SSS similarity criterion.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

In an equilateral triangle ABC if AD ⊥ BC, then
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
