Advertisements
Advertisements
Question
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

Solution
In Δ ABC, it is given that DE ∥ BC.
Applying Thales’ theorem, we get:
`(AD)/(DB)=(AE)/(EC)`
∵ AD = 3.6 cm , AB = 10 cm, AE = 4.5cm
∴ DB = 10 − 3.6 = 6.4cm
Or,` 3.6/6.4=4.5/(EC)`
Or, EC =`( 6.4×4.5)/3.6`
Or, EC= 8 cm
Thus, AC = AE + EC
= 4.5 + 8 = 12.5 cm
APPEARS IN
RELATED QUESTIONS
In below figure, If AB || CD, find the value of x.
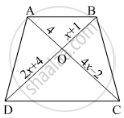
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
In the given figure, DE || BD. Determine AC and AE.

In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
