Advertisements
Advertisements
प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

उत्तर
In Δ ABC, it is given that DE ∥ BC.
Applying Thales’ theorem, we get:
`(AD)/(DB)=(AE)/(EC)`
∵ AD = 3.6 cm , AB = 10 cm, AE = 4.5cm
∴ DB = 10 − 3.6 = 6.4cm
Or,` 3.6/6.4=4.5/(EC)`
Or, EC =`( 6.4×4.5)/3.6`
Or, EC= 8 cm
Thus, AC = AE + EC
= 4.5 + 8 = 12.5 cm
APPEARS IN
संबंधित प्रश्न
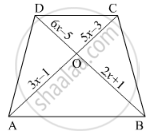
In the below figure, If AB || CD, find the value of x.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
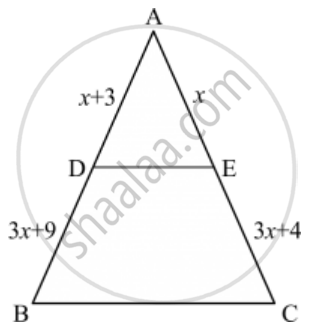
In the given figure, the value of x for which DE || AB is
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
